Eine sehr verbreitete Analyse in der Logistik ist die ABC-XYZ-Analyse. Diese Analyse spielt vor allem in der Beschaffungslogistik sowie in der Distributionslogistik eine entscheidende Rolle bei der Festlegung von Strategien zu Reduzierung des Einkaufaufwandes sowie der Lagerbestände (Kapitalbindung).
- Beschaffungslogistik (Einkauf): Es sollen möglichst wenige, wertschaffende Teile/Rohstoffe eingekauft werden, welche möglichst regelmäßig eingekauft werden (hohe Versorgungsstabilität entspricht geringes Einkaufsrisiko)
- Distributionslogistik (Verkauf): Es sollen möglichst nur Teile im Lager stehen, welche einen hohen Wert (hohe Marge pro Verkaufstransaktion) haben und möglichst regelmäßig von der Kundschaft abgenommen werden (hohe Vertriebsstabilität entspricht geringes Abnahmerisiko)
Für die ABC-XYZ-Analyse ist die Durchführung von vorhergehenden ABC- und XYZ-Analysen notwendig. Diese sind mit gängigen ERP-Systemen oft mit wenigen Klicks machbar, können jedoch auch per Excel errechnet werden.
ABC-Analyse
Es werden alle Lagerbestände oder Einkaufsvolumen gesammelt und nach Produkten/Teilen/Rohstoffen oder Produkt-/Bau-/Rohstoffgruppen sortiert. Die Sortierung erfolgt nach Lagerwert bzw. Einkaufswert (Abwärtssortierung). An erster Stelle steht demnach das wertvollste (teuerste) Produkt. Dieses wird in das Diagramm als Punkt oder Säule als erstes eingetragen (auf die X-Achse, ganz links). Die nachfolgenden, immer weniger wertvoll werdenden Produkte werden dann nach rechts verlaufend auf der X-Achse eingetragen. Die Wertsummen (Y-Achse) werden dabei kumuliert.
| Nr. | Produkt | Wert [€] | kummulierter Wert | Menge | kumulierte Menge |
|---|---|---|---|---|---|
| 1 | C3B1232343 | 15000 | 15000 | 22 | 22 |
| 2 | C1B1343323 | 14000 | 29000 | 18 | 40 |
| 3 | C2B5467567 | 11000 | 40000 | 45 | 85 |
| 4 | C3B1533369 | 10800 | 50800 | 78 | 163 |
| 5 | C7B1453243 | 10600 | 61400 | 65 | 228 |
| 6 | C3B1221233 | 9900 | 71300 | 155 | 383 |
| … | |||||
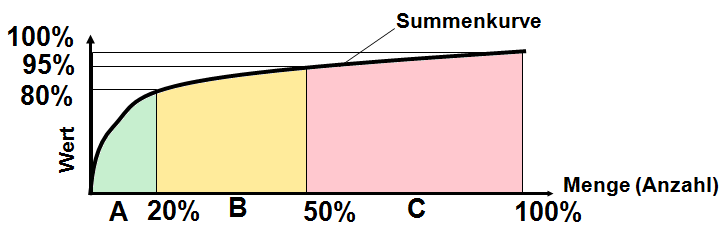
Die Daten werden dann in ein kartesisches Koordinaten-Diagramm übertragen, erst dann werden die Produkte in eine der Klassen A, B oder C eingeordnet. Durch die Sortierung nach Wert liegen die Produkte bereits in ihrer Klasse, definiert werden müssen nur die Grenzen der Klassen nach kumulierten Werten festgelegt werden. Die Grenzen liegen im ideal-typischen Fall bei 0-80% für Klasse A, 80-95% für Klasse B und 95-100% für Klasse C. Es ist jedoch notwendig, die Klassen nicht im Vorfeld festzulegen, sondern die Summenkurve im Diagramm zu betrachten und markante Tangenten (Steigungen) zu suchen.
A-Materialien haben einen geringen mengenmäßigen, aber einen hohen wertmäßigen Anteil
B-Materialien haben einen mittleren mengenmäßigen und wertmäßigen Anteil
C-Materialien haben einen hohen mengenmäßigen, jedoch nur einen geringen wertmäßigen Anteil
Im obigen Diagramm ist eine ABC-Analyse mit ideal-typischem Verlauf dargestellt. 20% der Teile (Anzahl) sind für 80% der Werte (Umsatz oder Kapitalbindung) verantwortlich (Klasse A), 50% der Teile für nur 5% der Werte (Klasse C). Dazwischen liegt die Klasse B mit 30% mengenmäßigen und 15% wertmäßigen Anteil an allen Produkten.
XYZ-Analyse
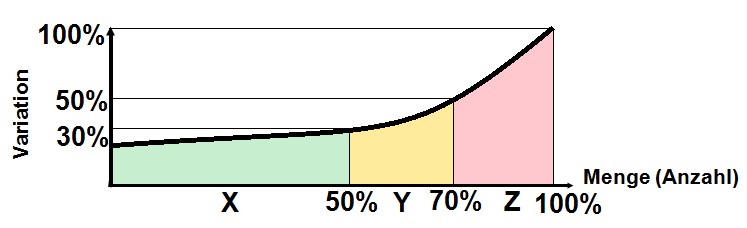
Die XYZ-Analyse beginnt mit der Ermittlung der Variationskoeffizienten der einzelnen Artikel/Materialien/Produkte. Nach der Sammlung der Daten erfolgt eine Sortierung der Artikel nach aufsteigendem Variationskoeffizienten. Der Variationskoeffizient V ist ein Maß für die relative Streuung der Liefer-/Verbrauchshäufigkeit eines Artikels um einen Mittelwert. Die Ermittlung erfolgt durch Division der Standardabweichung durch den Mittelwert der Liefer-/Verbrauchshäufigkeit.
Der Verlauf der Variationskoeffizienten wird in einem kartesischen Koordinatensystem visualisiert. Die Erstellung des Diagramms erfolgt nach dem gleichen Schema, wie bei der ABC-Analyse.
X-Materialien haben eine hohe Vorhersagegenauigkeit (konstant-regelmäßiger Verbrauch)
Y-Materialien haben eine mittlere Vorhersagegenauigkeit (saisonal-regelmäßiger Verbrauch)
Z-Materialien haben eine geringe Vorhersagegenauigkeit (unregelmäßiger Verbrauch)
Auswertung der ABC-XYZ-Analyse
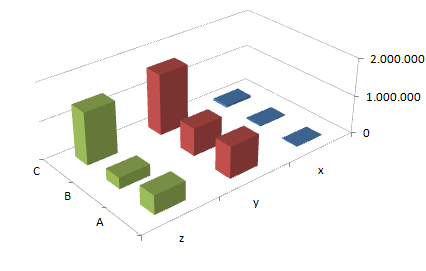
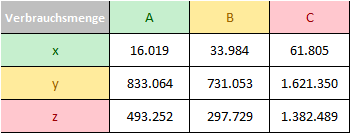
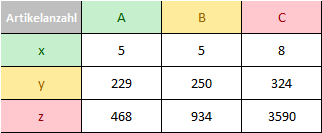
In einer Matrix können ABC- und XYZ-Analyse zusammengeführt werden. Von Interesse sind die Mengen (Anzahl) an Artikeln und deren Verteilung in der ABC-XYZ-Matrix.
Am besten lässt sich die Verteilung nicht nur quantitativ, sondern auch grafisch dargestellt ablesen.
Für eine grafische Auswertung eignet sich besonders gut ein dreidimensionales Säulendiagramm. Eine solche Visualisierung bieten moderne ERP-Systeme oder können auch in Excel erstellt werden.
 |
 |
Abzuleitende Strategien
Beliebte Artikel – einfach zu beschaffen und hoher Wert
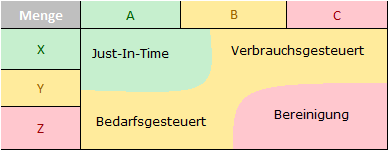
Die liebsten Teile der Einkaufs-/Vertriebsplaner sind die Teile aus dem Überschneidungsbereich der Klassen A und X. Diese Teile sind leicht zu planen, da regelmäßig geliefert und verbraucht und einfach zu beschaffen (da attraktives Geschäft für Lieferanten) sowie gewinnbringend verkaufbar. Der Kauf auf Lager ist möglich. Soll die Kapitalbindung reduziert werden, ist eine Just-In-Time-Steuerung vorzuziehen.
Unbeliebte Teile – schwierig zu beschaffen, hoher Wert
Artikel aus dem Überschneidungsbereich der Klassen A und Z sollten bedarfsgesteuert eingekauft, geplant und vertrieben werden. Diese Teile lohnen nur wegen ihres relativ hohen Wertes.
Unbeliebte Teile – einfach zu beschaffen, jedoch geringer Wert
Artikel aus dem Überschneidungsbereich der Klassen C und X sollten verbrauchsgesteuert beschafft werden. Die Teile haben nur einen relativ geringen Wert, sind aber einfach zu planen und zu beschaffen. Auf Grund der gut planbaren und oft hohen Volumen sind diese Teile für Lieferanten mittelmäßig interessant.
Unbeliebte Teile – schwierig zu beschaffen, geringer Wert
Artikel aus dem Überschneidungsbereich der Klassen C und Z sind sehr schwierig zu beschaffen und häufig Thema für schwierige Projekteinkäufe. Lieferanten bieten diese Artikel kaum an, da sie unattraktiv sind. Bei einer Serienfertigung sollte eine Programmbereinigung (z. B. durch Standardisierung) in Erwägung gezogen werden, so dass diese Teile auf das absolut Nötigste reduziert werden!

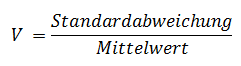
6 Gedanken zu „ABC und XYZ – Analyse“
Kommentare sind geschlossen.