Komplexe Zahlen erweitern den reellen Zahlenbereich. Mit komplexen Zahlen können Berechnungen vereinfacht werden. Mit komplexen Zahlen lässt sich auch die Quadratwurzel aus einer negativen Zahl berechnen.
Komplexe Zahlen bestehen aus einem Imaginärteil und einem Realteil.
Der Imaginärteil hat in der Mathematik die Einheit i oder j, in der Elektrotechnik generell immer j (um Verwechselungen mit „i“ für den Wechselstrom zu vermeiden).
j0=1
j1=j
j²=-1
j³=-j
j4=j1=j
j-1=1/j=j/j²=j/-1=-j
______________________________________________________
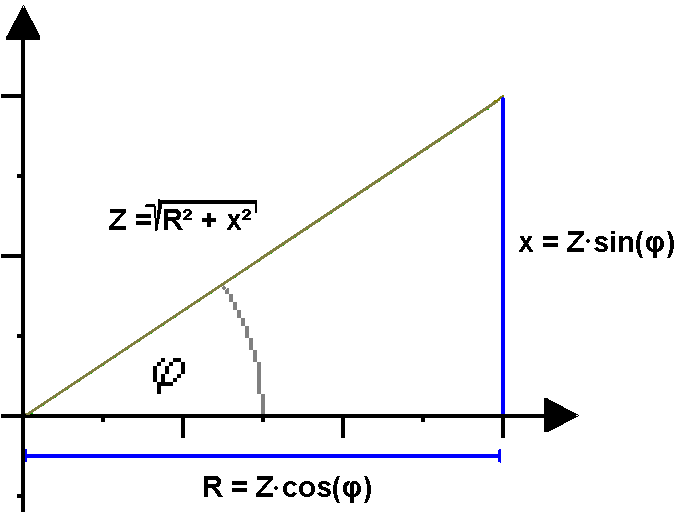
Imaginär- und Realteil einer komplexen Zahl können im kartesischen Koordinatensystem und auch im Polarkoordinatensystem veranschaulicht werden.
Diese Darstellungsweise, welche im kartesischen Koordinatensystem leicht nachvollzogen werden kann, kann mit Hilfe des Satzes von Pythagora und der Funktion Arkustangens in die Polarkoordinatenform umgewandelt werden.
Die Polarform zeigt das Produkt aus R und der Exponentialfunktion e.
Bei sinusförmigen Wechselstrom gilt für φ die Funktion der Zeit ωt (Kreisfrequenz ω multipliziert mit der Zeit t).
Über Addition und Subtraktion hinausgehende Berechnungen, werden am einfachsten in der Polarform vorgenommen.
Das Potenzieren einer komplexen Zahl ist in der Polarform einfach durchzuführen.
Multiplikation und Division:
Die Differentiation einer komplexen Zahl entspricht einer Drehung um 90° in positiver Richtung. Die Integration beschreibt den umgekehrten Weg, die Drehung des Winkels in negativer Richtung.
Bei ωt eingesetzt für φ gilt dann: