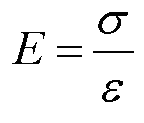In der Umwelt sind Körper nie absolut starr, anders als man es bei der Berechnung z.B. in der Statik gerne hätte. Die Körper aus bestimmten Materialien sind unterschiedlich beschaffen und reagieren auf Beanspruchung unterschiedlich.
Für Ingenieure ist es jedoch von äußerster Wichtigkeit, das Verhalten eines Materials bei Beanspruchung einschätzen zu können.
Bei Zug reagieren Körper mehr oder weniger (da materialabhängig) mit Dehnung. Welcher Grad der Dehnung und wann welche Dehnstufe (elastische Dehnung, plastische Dehnung, Bruch) erreich wird, wird mit einem Zugversuch im Labor getestet.
Beim Zugversuch werden Objekte eingespannt und an ihnen nach einem standarisiertem Verfahren gezogen.
Der Zugversuch setzt die Dehnung δ und die Spannung ε ins Verhältnis, es resultiert ein Wert (E-Modul) der Auskunft über die Elastizität bei Spannungsanstieg gibt. Der E-Modul wird i.d.R. mit der Einheit kN/mm2 angegeben.
[ad#Google Adsense Square]
Die Dehnung ε ist wiederum das Verhältnis aus der durch eine Beanspruchung entstandenen Längenänderung und der Ausgangslänge, die vor der Beanspruchung existierte.
Mit dem Zugversuch können die Zugfestigkeit, Bruchdehnung, Streckgrenze und Proportionalitätsgrenze eines Materials bzw. eines Objekts aus einem bestimmten Material ermittelt werden. Mit dem Zugversuch bzw. den Ergebnissen aus dem Zugversuch kann ein Spannungs-Dehnungs-Diagramm konstruiert werden.
Die Spannung δ ist das Verhältnis aus einwirkende Kraft F und die Fläche A, auf die die Kraft wirkt.
Das Lese-Prinzip des Spannungs-Dehnungs-Diagramm ist einfach: Bei steigender Spannung, steigt die Dehnung. Die Dehnung kann beispielsweise linear ansteigen oder auch sehr ruckartig voranschreiten.
Grundsätzlich beginnt die Dehnung mit einem linearen Verhalten. In dem linearen Bereich gilt das Gesetz von Hooke (Hookesche Gesetz).
Der Wert des E-Moduls selbst ist also die anfängliche Steigung des Graphen im Spannungs-Dehnungs-Diagramm.
Spannungs-Dehnungs-Diagramm
Der Winkel α ist abhängig von der Sprödigkeit. Ein kleinerer Winkel α bedeutet, dass das Material eher duktil ist.
Ein weiterer interessanter Faktor ist die Querdehnung, dies ist die Dehnung, die senkrecht zur Beanspruchungsrichtung geschieht.
Die Poissonzahl v (oder μ), oder auch Querdehnzahl v (μ), ist das Verhältnis aus der Elastizität des Querschnitts εq und der Elastizität (in Beanspruchungsrichtung) ε.
Die Querschnittselastizität berechnet sich aus den Verhältnis des ursprünglichen Durchmessers und der Änderung des Durchmessers nach der Beanspruchung kurz vor Bruch.
Die Poissonzahl ist eine Materialkonstante und dimensionslos (wie auch z.B. der Reibungskoeffizient).
Die Elastizität (E-Modul) und die Poissonzahl sind wichtige Kennzahlen in der Festigkeitslehre.
Beispiele für E-Modul-Werte und Poissonzahlen:
- Titan mit 105 kN/mm2 und einer Poissonzahl von 0,34
- Glas mit zwischen 50 und 90 kN/mm2 und einer Poissonzahl zwischen 0,18 und 0,30
- Stahl (Ferrit) mit 210 kN/mm2 und einer Poissonzahl zwischen 0,26 und 0,28
Hinweise:
Die Elastizität ist nicht nur von der beanspruchenden Kraft abhängig, sondern auch von der Temperatur.
Die Ursache einer Dehnung kann, neben einer Krafteinwirkung, auch eine veränderte Material-Temperatur sein.
Die Zähigkeit des Materials wird nicht mit dem Zugversuch, sondern mit dem Kerbschlagversuch zur Überprüfung der Kerbschlagzähigkeit in Erfahrung gebracht.